In der Wissenschaft geht es darum, beobachtete Phänomene so auf essentielle Prozesse zu vereinfachen und auszudrücken, dass andere Wissenschaftler dieses Modell verstehen, adaptieren oder mit ihrem eigenen Modell vergleichen können. Die Ausdrucksweise, mit der das Modell formuliert wird, nenne ich hier ganz einfach Sprache. Sie ist nicht nur die Ausdrucksweise in Worten wie in diesem Text – auch genannt „natürliche Sprache” –, sondern Körpersprache, Bilder, Programmiersprache und, gerade in der Wissenschaft, auch Mathematik.
Laut Wikipedia versteht man unter Sprache „im allgemeinen Sinn alle komplexen Systeme der Kommunikation“. Phänomene in der Sprache der Mathematik auszudrücken (hier ist vor allem Algebra gemeint), ist der Goldstandard der Modellierung in den Wirtschaftswissenschaften. Für Wirtschaftspolitik relevante Phänomene wie die Anpassung von Preisen und Mengen auf Märkten als Reaktion auf alle möglichen äußeren Einflüsse, wie staatliche Anreize oder Änderungen an vorgelagerten Märkten, können durch mathematische Modelle erfolgreich antizipiert werden.
Doch viele wichtige und interessante Phänomene lassen sich mit der in der Ökonomik verwendeten Mathematik nicht modellieren. Phänomene wie der technologische Wandel, das Entstehen und die Evolution ökonomischer Strukturen wie etwa der Wandel von Planwirtschaft zu Marktwirtschaft lassen Leerstellen im Kanon der mathematischen Modelle in den Wirtschaftswissenschaften. Die genannten Phänomene zeichnen sich durch ihre Komplexität und Dynamik aus. Sie allein mit Mathematik zu modellieren ist eine Herausforderung, die bisher scheitert. Wenn man sich aktuell der Modellierung dieser Phänomene in ihrer ganzen Komplexität und Dynamik widmet, dann mithilfe natürlicher Sprache.
Mathematik zur Modellierung zu verwenden hat einen guten Grund: Die Modelle sind dadurch leicht vergleichbar – Gemeinsamkeiten und Unterschiede lassen sich schlicht besser finden als bei in natürlicher Sprache ausgedrückten Modellen. Doch die Fokussierung auf mathematische Modelle in den Wirtschaftswissenschaften führt zu einer problematischen Situation: Komplexe, dynamische Phänomene werden in wirtschaftswissenschaftlichen Lehrveranstaltungen nicht behandelt, da sie sich nicht in ein Korsett aus Gleichungen zwängen lassen. Wenn Lehrende es selbst schwierig finden, nicht-mathematische Modelle zu vermitteln (Roos, 2017), dann scheint die Dominanz der Mathematik einem Phänomen zu entsprechen, welches ÖkonomInnen nur zu genau kennen: Ein Lock-In in die Sprache der Mathematik in den Wirtschaftswissenschaften verhindert die Modellierung komplexer, dynamischer Phänomene in einer geeigneten alternativen Sprache. So kommt es in der Ökonomik zu einer beachtlichen Diskrepanz zwischen dem, was wir modellieren können und dem, was wir modellieren sollten.
Die Grenzen der Mathematik
Die Kritik, dass mathematische Modelle nur einen Teil unserer ökonomischen Welt erklären können, ist nicht neu und wurde bereits vielfach vertreten. So bemängelt der Ökonom Michael Roos, dass Volkswirte kaum in natürlicher Sprache kommunizieren: „Ökonomen beschäftigen sich nicht oder nicht ausreichend mit einigen gesellschaftlich relevanten Problemen, weil sich diese nicht mathematisieren lassen.“ (Roos, 2017). Brian Arthur argumentiert in ähnlicher Weise (Arthur, 2021) und präzisiert das Argument noch. In Algebraischer Mathematik könnten Quantitäten und ihre Beziehungen, Arthur nennt das „Substantive“, in natürlicher Weise ausgedrückt werden. Doch Prozesse und Wandel seien wie Verben – und algebraische Mathematik sei ungeeignet, um diese auszudrücken. Für Arthur sind Algorithmen die geeignete Sprache, um solche komplexen, dynamischen Phänomene formal auszudrücken.
Kritik an den „blinden Flecken der Ökonomik“ spiegelt sich regelmäßig in der von Studierenden geäußerten Unzufriedenheit mit ökonomischer Lehre wieder (Theile, 2014), (Plickert, 2016), (Herrmann, 2016). Die Lücke zwischen den modellierten Phänomenen und den Phänomenen, für die Studierende sich interessieren und weswegen sie ein VWL-Studium beginnen, ist aufgrund des hohen Anteils algebraischer Mathematik in Lehrveranstaltungen groß. Den Studierenden die Beschreibung komplexer, dynamischer Phänomene zu vermitteln, wird Anderen überlassen: Etwa den KolumnistInnen in Wirtschaftszeitungen, aber auch den anderen Sozialwissenschaften, vor allem der Soziologie und den Politikwissenschaften. Wie der eben zitierte Michael Roos beobachtet, sorgt die unterschiedliche Sprache in den Gesellschaftswissenschaften nebenbei auch dafür, dass die Wirtschaftswissenschaften, mit ihrer Mathematik, und die anderen Disziplinen, mit ihrer natürlichen Sprache, nicht miteinander kommunizieren können.
Doch welche ökonomischen Phänomene können mit Mathematik modelliert werden? Wann sind Algorithmen zur Modellierung komplexer, dynamischer Phänomene geeignet? Und wann sind Phänomene so komplex und dynamisch, dass nur noch natürliche Sprache hilft?
Grafik 1 soll eine Orientierung geben. Auf der zweidimensionalen Karte, welche durch die Variablen Komplexität und Dynamik aufgespannt wird, liegen verschiedene ökonomische Phänomene, etwa Preis- und Mengenanpassung auf Märkten, die Dynamik von Finanzmärkten, die Reaktion des Bankennetzwerks auf Schocks oder der technologischer Wandel. Farbige Schraffuren im Hintergrund geben an in welchen Sprachen diese Phänomene jeweils modelliert werden können. Die Landschaft auf der Karte gliedert sich in drei Sprachen: Mathematik, natürliche Sprache und Algorithmen. Entlang der eingezeichneten Wege wird der Beitrag nun durch ökonomische Phänomene als Orte auf dieser Karte führen – von den einfachen Systemen ohne eigene Dynamik zu den komplexen dynamischen Systemen. Dabei wird erörtert, welche Sprachen zur Modellierung der jeweiligen Phänomene geeignet sind.
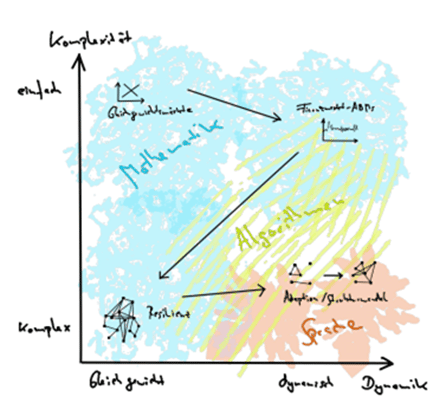
Startpunkt sind die einfachen Systeme ohne eigene Dynamik (obere linke Ecke). Wie bereits zuvor erwähnt wurde, sind das die Systeme auf welche sich aktuelle ökonomische Lehrveranstaltungen fokussieren: Die Anpassung von Preisen und Mengen an Gleichgewichtsmärkten als Reaktion auf Schocks oder auch die Reaktion aggregierter makroökonomischer Variablen, welche sich in einem Gleichgewicht befinden, auf Schocks.
Rechts davon, im Bereich der etwas komplexere Systeme mit hoher Dynamik sind Finanzmärkte platziert. Aufgrund der Interaktion verschiedener Händlergruppen mit unterschiedlichen Strategien bilden sich dort sehr komplexe Preisdynamiken. In einfachster Form können diese Prozesse mittels Mathematik (Differentialgleichungen) beschrieben werden. Bei komplexeren Finanzmarktmodellen kommen auch Algorithmen zum Einsatz. Insbesondere wenn evolutionäre Algorithmen verwendet werden, welche es den Agenten innerhalb des Modells erlauben ihre Handelsstrategien anzupassen, rutschen die Finanzmarkt-ABMs (Agentenbasierte Modelle) nach unten in Richtung Adaption. Solche Modelle von Märkten außerhalb eines Gleichgewichts finden selten Eingang in ökonomische Lehrveranstaltungen.
Eine weitere Kategorie sind komplexe Systeme ohne eigene Dynamik (untere linke Ecke). Oft sind wir als Gesellschaft daran interessiert solche Systeme, etwa das Finanzsystem oder das Produktionsnetzwerk, in ihrer grundsätzlichen Struktur zu erhalten und gegen Schocks zu wappnen. Mit der durch die Corona-Pandemie und den Russland-Ukraine-Krieg entstandenen Lieferkettenprobleme und Versorgungsengpässe steht das Thema Resilienz ganz oben auf der wirtschaftspolitischen Agenda. Zuvor hatten bereits Reaktionen auf die globale Finanzkrise 2007/2008 Modelle hervorgebracht, welche die Stabilität des Bankensystems untersuchen. Ein 2017 im Wirtschaftsdienst erschienener Artikel bietet eine gute Einordnung des Konzepts Resilienz in den ökonomischen Kontext (Brinkmann et al., 2017). Leider sind diese Themen in Lehrveranstaltungen bisher kaum angekommen. Resilienz wird mithilfe komplexer Netzwerke modelliert. Dabei kommen Mathematik (Graphentheorie) aber auch Algorithmen zum Einsatz.
Der letzte Ort auf der Karte (unten rechts) sind die komplexen, dynamischen Phänomene: Ich nenne sie „Adaption und Strukturwandel“. Diese werden bisher vor allem mittels natürlicher Sprache modelliert. So füllen Bücher zum Strukturwandel von sozialistischen Staaten zu kapitalistischen Systemen zwar die Regale von Bibliotheken, aber Thema in Lehrbüchern oder Lehrveranstaltungen der Wirtschaftswissenschaften sind solche fundamentalen Transformationen eines Wirtschaftssystems nicht. Für die heute stark formalisierte Ökonomik sind derartige Beschreibungen zu unpräzise, um in die Disziplin zu passen. Dabei wäre es gerade in einer Zeit, in der es als sicher gilt, dass der Klimawandel und der Verlust natürlicher Systeme großen Strukturwandel hervorrufen werden, immens wichtig, sich mit solchen Phänomenen in den Wirtschaftswissenschaften intensiv zu befassen.
Sollen wir also die formale Ausdrucksweise mittels Mathematik aufgeben und uns auf eine flexiblere Modellierung mittels natürlicher Sprache zurückbesinnen? Das ist wohl weder vollständig möglich noch nötig. Zum einen wird sich der starke Lock-In in Mathematik als Standardsprache der Ökonomik schwer zugunsten der Modellierung mit natürlicher Sprache aufbrechen lassen. Zum anderen hat sich mit der Etablierung von Computern eine neue Sprache herausgebildet: Algorithmen als eigenständige Sprache zwischen Mathematik und natürlicher Sprache machen es mehr und mehr möglich, komplexe, dynamische Phänomene stärker formalisiert zu modellieren als dies die natürliche Sprache kann.
Die Stärke von Algorithmen liegt in der Modellierung von Prozessen, den „ökonomischen Verben“ (Arthur). Drei Exemplare solcher Prozesse komplexer Systeme sollen hier beispielhaft vorgestellt werden. Der erste Prozess nennt sich preferential attachement. Er ist knapp gesagt eine Formalisierung der biblischen Wendung „wer schon hat, dem wird gegeben“. Ein Anwendungsfall sind Zitationen: Autoren, welche schon häufig zitiert werden, haben eine höhere Wahrscheinlichkeit noch ein weiteres Mal zitiert zu werden. In komplexen Systemen wird dieser Prozess oft verwendet, um zu untersuchen, wie sich neue Kanten in einem Netzwerk bilden.
Der zweite Prozess lässt sich als Verzweigungsprozess bezeichnen. Er kann beschreiben, wie zwei oder mehr bestehende Technologien zu einer neuen Technologie kombiniert werden (Sood et al., 2010; Fink und Teimouri, 2019; Fink, 2017). Der dritte Prozess ist Diffusion. Er beschreibt, wie sich etwa Informationen durch ein soziales Netzwerk verbreiten.
Zwar lassen sich alle drei Prozesse einzeln auch mathematisch formulieren – doch wenn sie miteinander interagieren, stößt die Mathematik an ihre Grenzen: Sobald sich die Prozesse abwechselnd wiederholen, verschachtelt ablaufen und ein Prozess den anderen anstößt, sind Algorithmen das Mittel der Wahl. Komplexe, dynamische Phänomene wie Strukturwandel und Adaption zeichnen sich durch die Kombination solcher einfacheren Prozesse aus. Algorithmen fungieren dabei als Ablaufplan, welche die Abfolge dieser Prozesse zum Beispiel hintereinander oder parallel schalten können. Transformationsprozesse wie die Energiewende sind ein Geflecht aus Informationsdiffusion, technologischem Wandel, Technologiediffusion und anderen Prozessen, die verschachtelt und zeitversetzt ablaufen und sich immer wieder gegenseitig anstoßen.
Konsequenzen für die Lehre
Ökonomische Forschung ist heute sehr vielfältig und beschäftigt sich – vor allem abseits der großen ökonomischen Journals – auch mit komplexen, dynamischen Phänomenen. Kritik an der Beschränkung ökonomischer Modelle auf einfache, statische Phänomene trifft vor allem die Lehre. Gibt es daher Schlussfolgerungen für die Lehre in den Wirtschaftswissenschaften?
Sinnvoll wäre es, schon heute verstärkt in Vorlesungen ökonomische Probleme in Algorithmen zu denken. Ganz konkret könnte man die Studierenden zuerst anleiten, wieder vermehrt sprachlich zu modellieren – die für uns Menschen, gerade wenn wir frisch aus der Schule kommen, natürlichste Weise zu modellieren. Am Anfang eines Seminars könnte also die Aufgabe stehen, ein ökonomisches Phänomen in einem Essay zu beschreiben. In einem nächsten Schritt sollten die Studierenden angeleitet werden, ihre Essays auf einfache Algorithmen zu reduzieren, welche die essentiellen Teile und Prozesse des Systems widerspiegeln. Ein naheliegender weiterer Schritt wäre, diesen Algorithmus in Computercode umzusetzen und die Ergebnisse der Simulation zu untersuchen. Gemeinsam mit den Studierenden könnte man auch versuchen, den Algorithmus in ein mathematisches Modell aus Differentialgleichungen oder, wenn es sich als Gleichgewichtsmodell formulieren lässt, aus Gleichungen, zu überführen.
Dieses Verfahren, ein komplexes, dynamisches Phänomen Stück für Stück auf einfachere Ausdrücke zu reduzieren, dürfte sich auch signifikant von der Erfahrung unterscheiden, welche Studierende in ihren Lehrveranstaltungen machen. Dort steht das mathematische Modell von vornherein im Vordergrund. Insofern liegen in der vermehrten Fokussierung auf Sprache und Algorithmen zur Modellierung zwei Chancen: zum einen endlich komplexe, dynamische Phänomene im Studium behandeln zu können, und zum anderen Studierenden eine Strategie zur eigenständigen Reduktion der Wirklichkeit an die Hand zu geben.
Zum Autor:
Lukas Jany studierte Environmental and Resource Economics an der CAU Kiel. Seit 2022 arbeitet er als Wissenschaftlicher Mitarbeiter beim Herkunftsnachweisregister für Strom aus erneuerbaren Energiequellen am Umweltbundesamt in Dessau-Roßlau und ist dabei vor allem mit Themen rund um die Stromkennzeichnung befasst.